Version: 3.4.0 - Date: 2024-03-15
Opt4J currently requires Java 21. To compile the following examples, you will need the respective JDK installed. Opt4J is distributed as single .zip file that can be downloaded from here. After extracting the files, the folder structure looks like this:
The application is launched with opt4j.bat under Windows and opt4j under Linux/Unix/OSX, respectively. Once started, it will appear the module configurator that allows to select an optimizer and problem as well as setting their parameters. For testing, load the test.config.xml and start the optimization with 'run'.
To develop custom optimization problems and algorithms for Opt4J, the files in the lib folder have to be on the classpath for compiling and starting the code. To start the module configurator manually, one has to run the class Opt4J which contains a corresponding main method.
To execute a specific configuration without the indirection over the user interface, you need to pass a configuration file to the application with the additional -s parameter to start the optimization. You may try this by executing the following command inside the bin folder:
> ./opt4j -s test.config.xml
If you write custom optimization problems and algorithms, you can drop a jar-file with the compiled code into the plugins folder and the corresponding modules are found automatically once Opt4J starts.
Use the batch.py script with python 2.x to run batch experiments for predefined configuration xml files. Execute 'python batch.py' to get further instructions how to use the script.
Custom optimization problems are typically defined by providing
three main classes:
(1) The Creator,
(2) the Decoder, and
(3) the Evaluator.
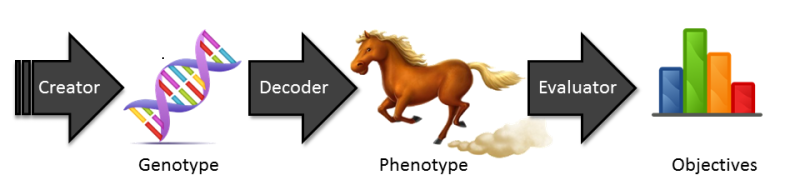
The functionality of these classes is illustrated in the following figure:

The creator provides random genotypes. A genotype is the genetic representation of an individual. The decoder transforms the genotype into the phenotype which represents all observable characteristics and components of the individual. Finally, based on the phenotype, the evaluator determines the objectives that represent the quality of the current individual.
By defining the creator, decoder, and evaluator (and implicitly the genotype and phenotype), the optimization algorithm can tackle the problem. In the following, it is shown how this can be done for two simple problems.
The hello world problem is inspired by the Watchmaker Framework tutorial. The goal is to optimize a string of eleven characters until this string results in the optimal solution "HELLO WORLD". For this purpose, we need to define the corresponding creator, decoder, and evaluator.
In the first step, we define the creator that implicitly defines the genotype:
public class HelloWorldCreator implements Creator<SelectGenotype<Character>> {
protected Character[] ALPHABET = { 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P',
'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z', ' ' };
protected Random random = new Random();
@Override
public SelectGenotype<Character> create() {
SelectGenotype<Character> genotype = new SelectGenotype<>(ALPHABET);
genotype.init(random, 11);
return genotype;
}
}
As mentioned, the task of the creator is to generate random genotype objects. In our case, we want to generate random strings with eleven characters. Here, we choose one of the predefined genotype classes that allows to select from a given alphabet and initialize it randomly with eleven (11) characters.
Note that Opt4J contains a set of predefined genotype classes (in the genotype package) that can also be combined and one should always choose from this set if possible instead of implementing custom genotypes that require an implementation of custom operators.
In the second step, we define the decoder that implicitly defines the phenotype:
public class HelloWorldDecoder implements Decoder<SelectGenotype<Character>, String> {
public String decode(SelectGenotype<Character> genotype) {
String phenotype = "";
for (int i = 0; i < genotype.size(); i++) {
phenotype += genotype.getValue(i);
}
return phenotype;
}
}
The task of the decoder is to convert our genotype into a phenotype which in our case is a string. This is done straightforward by copying the characters into a string.
In the third step, we define the evaluator:
public class HelloWorldEvaluator implements Evaluator<String> {
@Override
public Objectives evaluate(String phenotype) {
int value = 0;
for (int i = 0; i < phenotype.length(); i++) {
value += (phenotype.charAt(i) == "HELLO WORLD".charAt(i)) ? 1 : 0;
}
Objectives objectives = new Objectives();
objectives.add("objective", Sign.MAX, value);
return objectives;
}
}
The task of the evaluator is to determine the quality of one phenotype, i.e., one string. In our case, we count the number of matching characters when it is compared to "HELLO WORLD". Here, we want the number to be maximized. Note that we can add multiple objectives such that the problem becomes a multi-objective optimization problem.
Finally, we define a problem module:
public class HelloWorldModule extends ProblemModule {
protected void config() {
bindProblem(HelloWorldCreator.class, HelloWorldDecoder.class, HelloWorldEvaluator.class);
}
}
The problem module defines the problem and here particularly the corresponding creator, decoder, and evaluator. Once the module configurator is started, this problem module is automatically detected if it is on the classpath and we can select it.
You can also add additional evaluators and, thus, implicitly additional objectives by passing the additional evaluator class to the addEvaluator(..) method inside the config method.
The traveling salesman problem is a classic optimization problem. The goal is to minimize the length of a path that is required to visit a set of cities. The following code examples show a little bit of the dependency injection capabilities that are integrated into Opt4J by using Google Guice. It might be therefore also a good idea to have a short look at the tutorial of Guice if one plans to use dependency injection extensively. For this example, a profound understanding of Guice will not be necessary.
Let us start by defining our problem instance:
public class SalesmanProblem {
protected Set<City> cities = new HashSet<>();
public class City {
protected final double x;
protected final double y;
public City(double x, double y) {
this.x = x;
this.y = y;
}
public double getX() {
return x;
}
public double getY() {
return y;
}
}
@Inject
public SalesmanProblem(@Constant(value = "size") int size) {
Random random = new Random(0);
for (int i = 0; i < size; i++) {
final double x = random.nextDouble() * 100;
final double y = random.nextDouble() * 100;
final City city = new City(x, y);
cities.add(city);
}
}
public Set<City> getCities() {
return cities;
}
}
First we define that a city is given by an x and a y coordinate. In the constructor of our problem, we randomly generate a certain amount of cities that can later on be obtained. Here, the constructor is annotated with @Inject that is used by Guice to indicate which constructor will be used when the instance is created. The size argument in the constructor is annotated as constant that will be later set in the problem module.
The phenotype looks as follows:
public class SalesmanRoute extends ArrayList<City> {
}
In this case, we define a custom phenotype that is represented as a list of cities.
Now its again time to define our creator, decoder, and evaluator. Lets start with the creator:
public class SalesmanCreator implements Creator<PermutationGenotype<City>> {
protected final SalesmanProblem problem;
@Inject
public SalesmanCreator(SalesmanProblem problem) {
this.problem = problem;
}
@Override
public PermutationGenotype<City> create() {
PermutationGenotype<City> genotype = new PermutationGenotype<>();
for (City city : problem.getCities()) {
genotype.add(city);
}
Collections.shuffle(genotype);
return genotype;
}
}
The creator receives the problem instance in the constructor and saves it into a member variable. Here, we again see the @Inject annotation that is a little Guice magic to wire everything together. For the genotype, we use a predefined permutation genotype and add all cities. The permutation defines the order in which the cities will be visited by the traveling salesman. Note that each genotype is randomly shuffled before it is returned which is important since each genotype has initially to be generated completely randomly.
In the next step, we define the decoder:
public class SalesmanDecoder implements Decoder<PermutationGenotype<City>, SalesmanRoute> {
public SalesmanRoute decode(PermutationGenotype<City> genotype) {
SalesmanRoute salesmanRoute = new SalesmanRoute();
for (City city : genotype) {
salesmanRoute.add(city);
}
return salesmanRoute;
}
}
Here, we simply take the genotype and copy the cities in its current order into a route. Note that for more complex problems, a decoder can often do much more than just transforming the representation such as repairing, etc. Moreover, the decoder allows to implement different genotype representations of the same problem while the evaluator does not have to be changed at all since the decoder can transform each genetic representation into the same phenotype.
The evaluator looks as follows:
public class SalesmanEvaluator implements Evaluator<SalesmanRoute> {
public Objectives evaluate(SalesmanRoute salesmanRoute) {
double dist = 0;
for (int i = 0; i < salesmanRoute.size(); i++) {
City one = salesmanRoute.get(i);
City two = salesmanRoute.get((i + 1) % salesmanRoute.size());
dist += getEuclideanDistance(one, two);
}
Objectives objectives = new Objectives();
objectives.add("distance", Sign.MIN, dist);
return objectives;
}
private double getEuclideanDistance(City one, City two) {
final double x = one.getX() - two.getX();
final double y = one.getY() - two.getY();
return Math.sqrt(x * x + y * y);
}
}
The evaluator calculates the length of the current route and returns it as an objective that has to be minimized.
Finally we define the module as follows:
public class SalesmanModule extends ProblemModule {
@Constant(value = "size")
protected int size = 100;
public int getSize() {
return size;
}
public void setSize(int size) {
this.size = size;
}
public void config() {
bindProblem(SalesmanCreator.class, SalesmanDecoder.class, SalesmanEvaluator.class);
}
}
Additionally to setting the creator, decoder, and evaluator, we add a property size and annotate it as constant, corresponding to the argument in the constructor of the problem instance. Note that a correct property in the modules always requires a getter and setter method. If we start the configurator now, we will see that additionally to adding the problem module, we can also now set the size of our problem. The wiring of the problem, i.e., setting the size of the problem instance and passing the problem instance to the creator is now done by Guice and we do not have to burden ourselves with that.
Optimization in Opt4J follows a strict iterative pattern. All optimization algorithms have an initialization and an iterative optimization (next). Within these methods, the population of individuals has to be improved while the archive is updated in the background. As discussed before, each individual consists of a genotype, phenotype, and its objectives.
Opt4J already integrates many tools that are required to assemble optimization algorithms. The main ones are the following:
If you want to write custom optimizers, the following example will give you an idea how this is possible in Opt4J. On the other hand, it might be also worth to have a look into the source code and learn from reading the code of the existing algorithms.
This example shows how to write a very simple optimizer that is based on mutation only. The presented optimizer has a fixed population size of 100 and creates 25 offspring individuals from 25 parent individuals each generation by a mutate operation. The optimizer is implemented as follows:
public class MutateOptimizer implements IterativeOptimizer {
protected final IndividualFactory individualFactory;
protected final Mutate<Genotype> mutate;
protected final Copy<Genotype> copy;
protected final Selector selector;
private final Population population;
public static final int POPSIZE = 100;
public static final int OFFSIZE = 25;
@Inject
public MutateOptimizer(Population population, IndividualFactory individualFactory,
Selector selector, Mutate<Genotype> mutate, Copy<Genotype> copy) {
this.individualFactory = individualFactory;
this.mutate = mutate;
this.copy = copy;
this.selector = selector;
this.population = population;
}
public void initialize() throws TerminationException {
selector.init(OFFSIZE + POPSIZE);
}
public void next() throws TerminationException {
if (population.isEmpty()) {
for (int i = 0; i < POPSIZE; i++) {
population.add(individualFactory.create());
}
} else {
if (population.size() > POPSIZE) {
Collection<Individual> lames = selector.getLames(population.size() - POPSIZE,
population);
population.removeAll(lames);
}
Collection<Individual> parents = selector.getParents(OFFSIZE, population);
for (Individual parent : parents) {
Genotype genotype = copy.copy(parent.getGenotype());
mutate.mutate(genotype, 0.1);
Individual child = individualFactory.create(genotype);
population.add(child);
}
}
}
}
The initialization ensures that the selector is initialized. The optimization process is implemented in the next method. In the first iteration, the population is still empty and 100 new individuals are created and added. In all following iterations, first, the population is reduced to 100 by removing the worst individuals that are identified by the selector. Then, 25 parent individuals are determined by the selector and for each of these individuals, one individual is created by copying the genotype and mutating it. Finally, the new individuals are added to the population.
The optimization module looks as follows:
public class MutateOptimizerModule extends OptimizerModule {
@MaxIterations
protected int iterations = 1000;
public int getIterations() {
return iterations;
}
public void setIterations(int iterations) {
this.iterations = iterations;
}
@Override
public void config() {
bindIterativeOptimizer(MutateOptimizer.class);
}
}
The module requires to set the maximal number of iterations for the iterative optimizer by adding a property with the annotation @MaxIterations.
Opt4J is designed as a framework. However, it might also be comfortably used as a library in other projects. To embed Opt4J in other applications, the modules can be configured in Java, i.e., without the usage of the configurator. The following code snippet shows how to optimize the first DTLZ test function with an evolutionary algorithm from Java and, finally, how to obtain the best found solutions:
EvolutionaryAlgorithmModule ea = new EvolutionaryAlgorithmModule();
ea.setGenerations(500);
ea.setAlpha(100);
DTLZModule dtlz = new DTLZModule();
dtlz.setFunction(DTLZModule.Function.DTLZ1);
ViewerModule viewer = new ViewerModule();
viewer.setCloseOnStop(true);
Opt4JTask task = new Opt4JTask(false);
task.init(ea,dtlz,viewer);
try {
task.execute();
Archive archive = task.getInstance(Archive.class);
for (Individual individual : archive) {
// obtain the phenotype and objective, etc. of each individual
}
} catch (Exception e) {
e.printStackTrace();
} finally {
task.close();
}
First, you will have to construct the desired modules for the optimization process. An optimization process requires at least a ProblemModule which defines the Creator, Decoder, and Evaluator as described in Section 2. Here, the DTLZModule is used as an example. Also, an OptimizerModule is required which defines the optimization algorithm to use for the problem. In the example, the EvolutionaryAlgorithmModule is chosen but also the MutateOptimizerModule as developed in Section 3 could be used here. Additionally, the optional ViewerModule is created, which provides the GUI for the optimization process.
The
Opt4JTask
takes these modules and controls the optimization process.
Here, it is constructed with the parameter false that
indicates that the task is closed manually and not
automatically once the optimization stops. The Opt4JTask is
initialized with the modules. Now, it is possible to execute the task
(which is blocking in this case, but you can also start it in a
separate thread) and once the optimization is finished, you can obtain
the Archive to iterate over the best solutions. After closing the
task, obtaining instances like the Archive is not possible anymore.